Hi Everyone, today I want to talk about Union Find Problem. This is going to be a series covering:
- Union Find Problem (this blog)
- Solutions to Union Find (1): Quick Find
- Solutions to Union Find (2): Quick Union
- Solutions to Union Find (3): Weighted Quick Union
- Applications of Union Find (perculation and more)
- Cool project using Union Find
- Solving some competitive programming questions using Union Find
Each blog will try to cover very basic concepts behind the topic, and also what it’s all about.
Union Find Problem: Definition
Let’s define the problem first. It’s a problem where you need to find whether two points/objects are in a connected relationship (defined below) or not in a defined environment (where you know the relationships).
Connection Relationship is an equivalence relation, which means:
- It’s reflexive:
a ~ a(a is connected to itself) - It’s symmetric:
a ~ b iff b ~ a(a is connected to b iff b is connected to a OR if a is connected to b, b is also connected to a) - It’s transitive:
if a ~ b and b ~c then a ~ c(if a is connected to b, and b is connected to c, then a is connected to c)
And by connected, we just mean that there is a path between the two objects. My thinking around this problem is mostly surrounded by the plot of dynamic connectivity, where you want to find if there is a connection between 2 objects in a graph. These objects can be friends (whether A and B are friends or not in a circle - here circle is the environment).
Union Find: Problem, why study it?
It’s a name to a problem, but you must have encountered this in real life. Whether you are a friend to your ex, oh definitely not ;) (even if Union Find solution finds a connection, trust me - move on :P). Okay, on a serious note now:
Union Find Problem is seen in lots of applications:
- Perculation (example: if you pour water on the top of a tank having lots of cells/blocks - some are open, some are closed - will it reach the bottom?).
- I also see this as an application where you want to find if the leakage in a whole network of oil pipes will exit or if it will be blocked.
- Dynamic Connectivity: A very simple definition would be, whether there is a connection between two objects?
- You can see it’s application in social media, whether two objects (I know I should use humans but the whole internet objectifies you ;), hence objects ;)).
- Whether there is a connection between two places in a nation or not?
- Games (will be discussed later)
- and more…
Now it’s indeed a very interesting problem, and in this blog, I’ll show you a very basic implementation which I wrote before studying the algorithms which attempt to solve this problem.
Union Find breakdown: Union and Find
NOTE
All codes are written here in C++ and code is available here: https://github.com/krshrimali/Algorithms-All-In-One/.
Breaking it down to two functions, is really helpful:
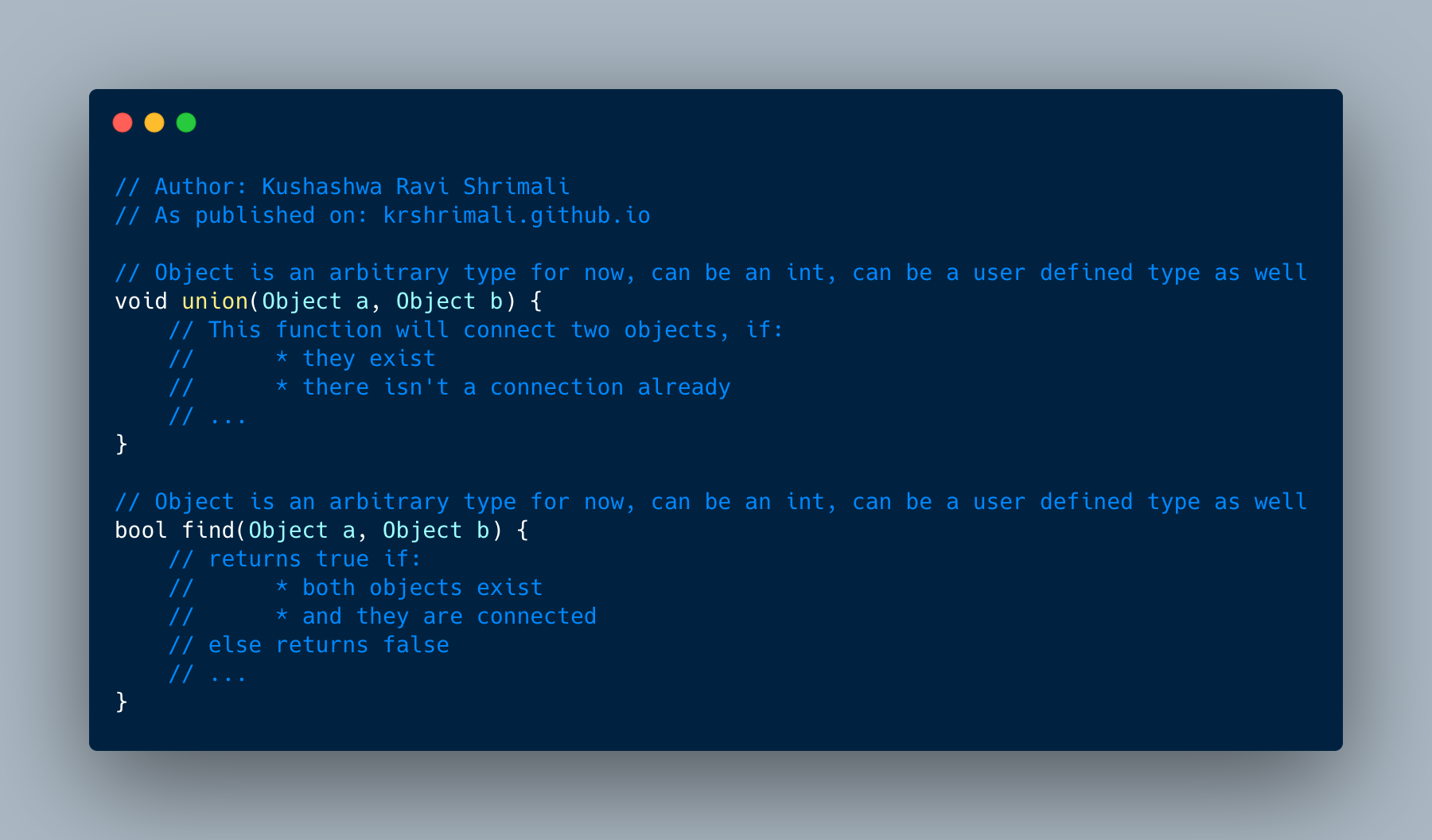
// Object is an arbitrary type for now, can be an int, can be a user defined type as well
void union(Object a, Object b) {
// This function will connect two objects, if:
// * they exist
// * there isn't a connection already
// ...
}
Similarly, the find function will try to find whether there is a connection between two objects:
// Object is an arbitrary type for now, can be an int, can be a user defined type as well
bool find(Object a, Object b) {
// returns true if:
// * both objects exist
// * and they are connected
// else returns false
// ...
}
Let’s try to setup the environment first, and we need to answer these two questions first:
- What should be the objects?
- Where are these objects stored?
I like thinking of this as a graph (environment) and points as objects. So let’s start implementing.
Implementation: Modelling
NOTE
This is a very basic implementation and first try presenting a naive solution to the problem, we’ll discuss better algorithms in next blogs.
The very first question you should ask yourself is, what data structures should be used for Graph and Point(s)? The way I’m thinking of solving this is:
- Each
Pointwill have(x, y)coordinates. (so coordinates will be it’s property) - Whenever two points are merged (
unionis called), the first point will append the second point in it’s list of connections.- So each
Pointobject will have a connection list. (std::vector?)
- So each
- Whenever
findis called, that is - there is an attempt to find if there is a connection between two points?- We just need to search if second point is there in the first point’s connection list. If it is, then there is a connection. And if not, then no connection.
- In python, I would have used a
dict, so I went ahead withstd::mapin C++, will help me not duplicating points.
So the Graph will be a std::map of Point, std::vector<Point>, which will look something like this:
// This is how graph will look like, in imagination
// Example:
// a is connected to b, c, d
// b is connected to a
(Point a, {Point b, Point c, Point d}),
(Point b, {Point a}),
...so on
As you can see, there will be a list mapped to each Point, we call that list: connection list.
Now, the Point can simply be a struct having int x, y as coordinates.
Implementation: Skeleton
Let’s create the skeleton now:
struct Point {
// x and y are the coordinates for each point
int x, y;
};
// Graph will contain Points, helper functions: union and merge
class Graph {
private:
std::map<Point, std::vector<Point>> graph;
public:
// We take references to avoid internal copies, const is used since we don't want these functions
// to modify these points in any way
void union_(const Point& a, const Point& b) {
// Use find utility function of std::map
if (this->graph.find(a) == this->graph.end()) {
// Not found
// Means create an entry in the graph, and add b to the connection list of a
this->graph[a] = {b};
} else {
// Found
// Append b to the connection list of a
this->graph.at(a).push_back(b);
}
}
// Are a and b connected? OR Is there a path b/w a and b?
bool find_(const Point& a, const Point& b) {
// First check if there is an Point a in the graph
if (this->graph.find(a) == this->graph.end()) {
std::cout << "Not found\n";
return false;
} else {
// Object found
std::vector<Point> connection_list = this->graph.at(a);
// Now find if b exists in the connection list, if yes then there is a connection
if (std::find(connection_list.begin(), connection_list.end(), b) != connection_list.end()) {
// b found
return true;
}
return false;
}
}
};
// Usage
int main() {
Graph g_sample;
struct Point p(2, 3);
struct Point q(3, 3);
struct Point r(4, 4);
// Add a connection for (p, q) and (p, r), for testing
g_sample.union_(p, q);
g_sample.union_(p, r);
std::cout << "Are p and q connected? Answer: " << sampleGraph.find_(p, q) << '\n'; // Expected: true
std::cout << "Are p and r connected? Answer: " << sampleGraph.find_(p, r) << '\n'; // Expected; true
std::cout << "Are q and r connected? Answer: " << sampleGraph.find_(q, r) << '\n'; // Expected: false
}
Now this is a great start, I won’t spend time explaining the code as the comments should help. In case you have queries, please feel free to open an issue here.
But this won’t compile. And the reason is, that when you are using std::find with user-defined types like Point, you need to define < operator or give it a comparator because it does some comparisons. Think of this like:
The compiler isn’t aware of how to do: Point(2, 3) < Point(3, 3)
Because for the compiler, both of these are an object. So we need to tell it explicitly, that hey! when you do < operation on Point objects, check their coordinates.
Final Implementation
The final code can be found here. There are a few TODOs in the code mentioned, and in case you want to pick them up, please create a PR for the same. :)
The code will change with time, so I’ll refrain copy-pasting it here.
Homework?
Let’s do this before I release the next blog:
- Analyze the algorithm used here, it’s time and space complexity.
- Address the TODOs in the code.
In case you are able to do this before my next blog, kudos to you! You might as well help creating a PR, that will be great.
Thank you for reading this blog. I hope you liked it! :)